B-tree와 B+tree (+ ISAM tree, Bulk Loading)

1)B-tree

B-tree 규칙

1)노드의 key가 k개면 자식 노드의 수는 k+1개 이다

2)모든 leaf 노드는 같은 level에 존재해야 한다

3)어느 노드는 왼쪽엔 자신보다 작은 값만, 오른쪽엔 자신보다 큰 값만을 지닌다

4)M차 B-tree는 한 노드당 최대 m개의 자식을 가질 수 있다.

 

더 들어가면

root 노드는 leaf 노드가 아닐 경우 항상 2개 이상의 자식을 갖는다

내부(root와 leaf 제외) 노드는 최소 m/2개의 서브 트리를 지닌다

이런 규칙도 존재

 

b-tree는 balanced tree로, 트리가 편향되지 않게하여 O(logN)이란 시간 복잡도를 유지한다

-> 그래서 모든 leaf 노드는 같은 level에 존재해야 한다

 

탐색의 경우 찾는 key가 현재 노드의 key보다 작으면 왼쪽, 크면 오른쪽으로 그래서 내려가며 찾는다

-> 그래서 모든 노드는 왼쪽엔 자신보다 작은 노드만, 오른쪽엔 큰 노드만 지녀야 한다

 

삽입은 leaf 노드에서부터 올라가며 진행된다

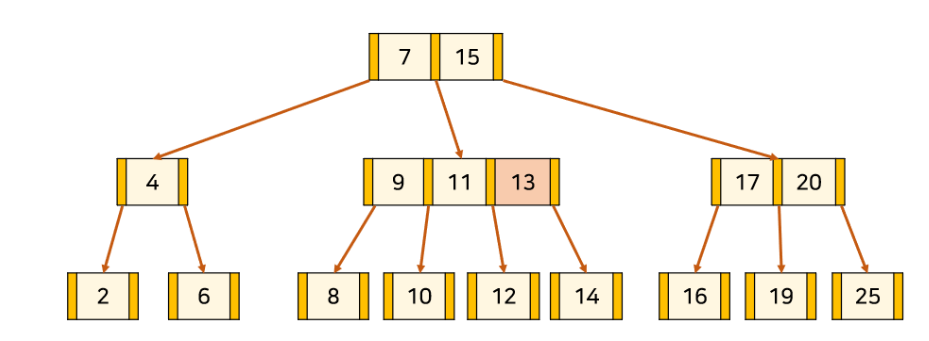
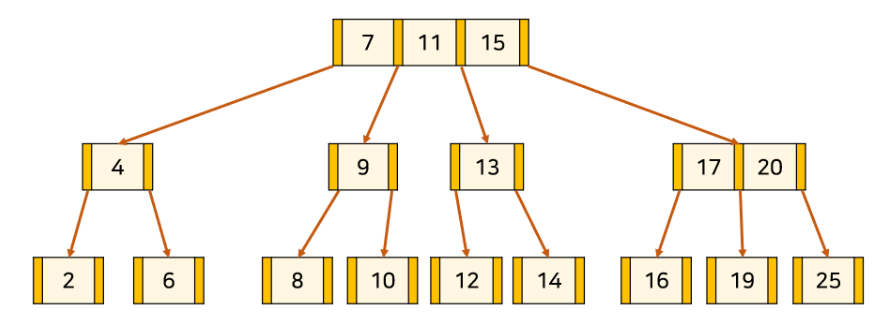
13 삽입

삽입의 경우 알맞은 leaf 노드에 넣고,

노드의 key 개수가 이미 최대면 가운데 값을 위로 올린다

 

 

key의 삭제의 경우 좀 복잡한데,

여러 경우의 수를 따져야한다

 

1)삭제할 key가 leaf 노드인 경우

1.해당 node의 key 개수가 최소가 아닌경우 -> 그냥 삭제하면 됨

2.해당 node의 key 개수가 최소인 경우 -> 형제 노드나 부모 노드로부터 하나 가져온다

 

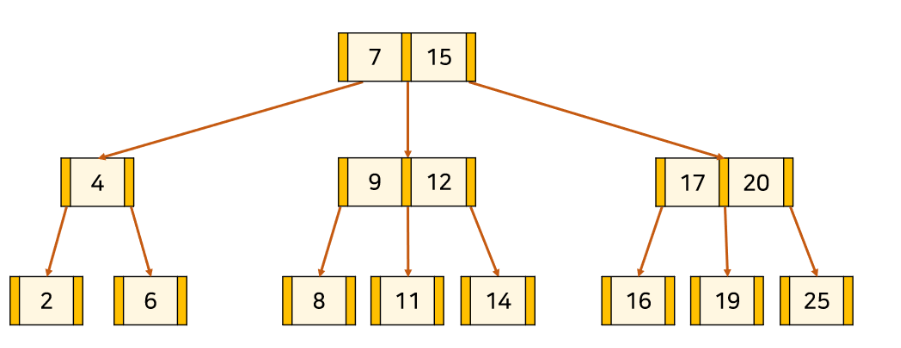
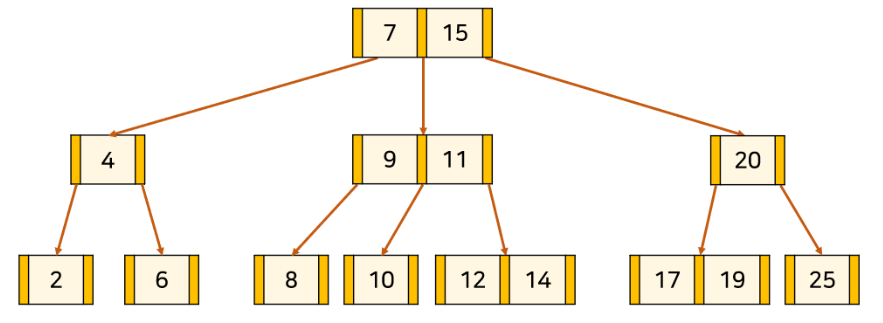
아무데서도 가져올 수 없을 경우 트리의 높이를 낮춰야 한다 (후술)

 

 

 

 

2)삭제한 key가 leaf 노드가 아닌 경우

1.현재 노드나 자식 노드의 key 수가 최소보다 큰 경우

삭제하려는 노드의 LMAX나 RMIN과 교체, 이후 리프 노드를 삭제하듯 삭제

*leaf 노드가 아닌 노드의 LMAX, RMIN은 무조건 leaf 노드

 

 

2.현재 node, 자식 노드 모두 key 수가 최소인 경우

-> 마찬가지로 트리를 재구조화하여 높이를 줄여야한다.

 

 

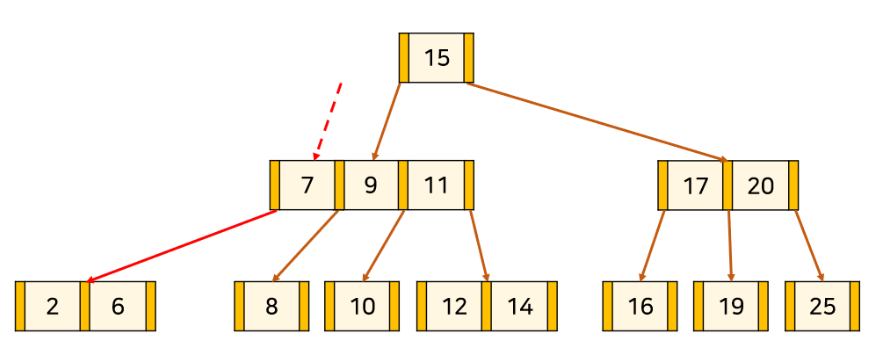
삭제하려는 key를 K라 할때,

1.K를 없애고 K의 자식 노드를 하나로 합친다

2.K의 부모 노드를 K의 형제 노드와 합쳐준다

3.둘을 부모 자식 관계가 되도록 연결한다

이때 부모 노드가 최대보다 크다면 마찬가지로 분할한다.

 

 

 

1.5)B*tree

b-tree에 규칙을 추가하여 overhead를 줄임

1)최소 노드의 개수가 m/2에서 2m/3으로

2)노드가 꽉 차면 형제노드로 먼저 보낸 뒤 불가능하면 부모 노드로 보냄

 

 

2)B+tree

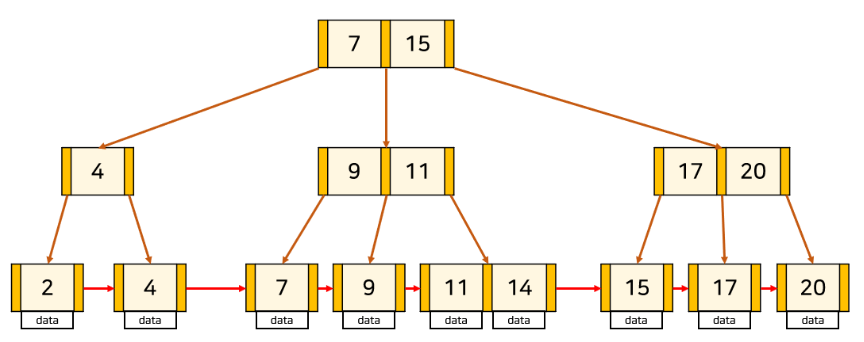
b-tree의 개선판이다.

데이터를 leaf 노드에만 저장해 트리의 높이를 낮추고 (상위 노드는 데이터가 없어서 더 많이 넣을 수 있다)

leaf 노드끼리 연결해놔 full scan을 빠르게 수행할 수 있다.

 

 

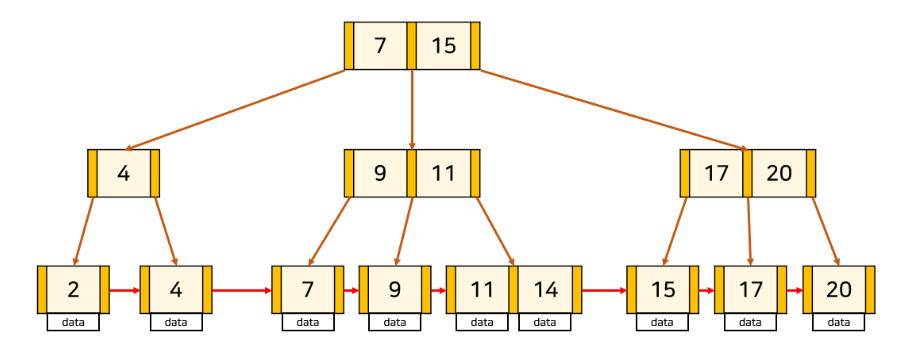
삽입의 경우 b-tree와 약간 다른데, 노드의 맨 앞에 삽입될 경우 부모 노드의 값을 수정해야한다

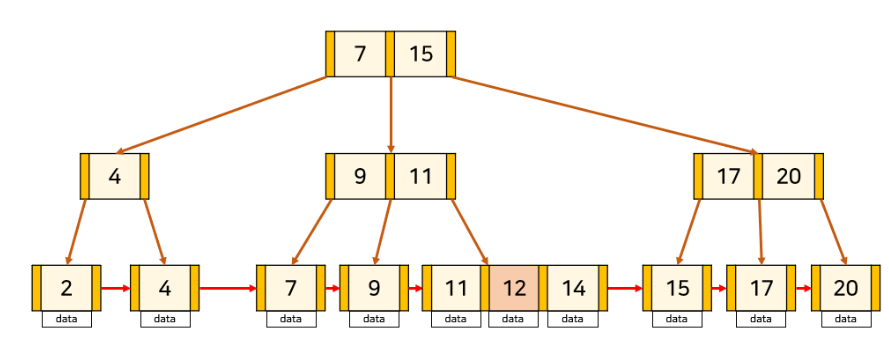
노드가 꽉 찼다면 똑같이 가운데 값을 올리나,

데이터는 leaf 노드에만 존재해야 하므로 해당 key를 오른쪽 노드에 추가로 붙인다.

 

 

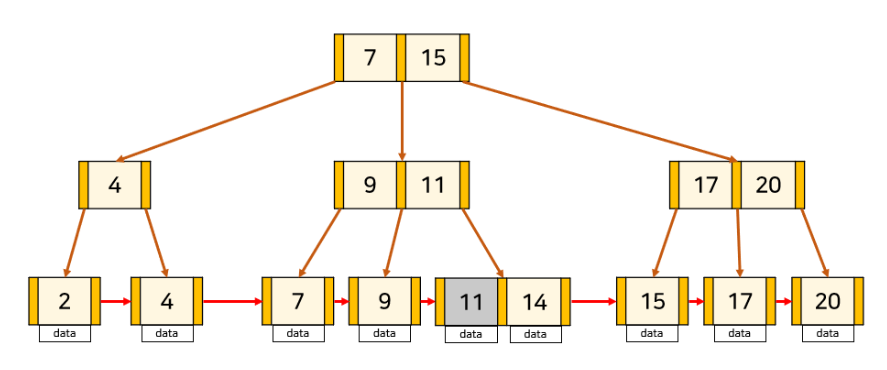
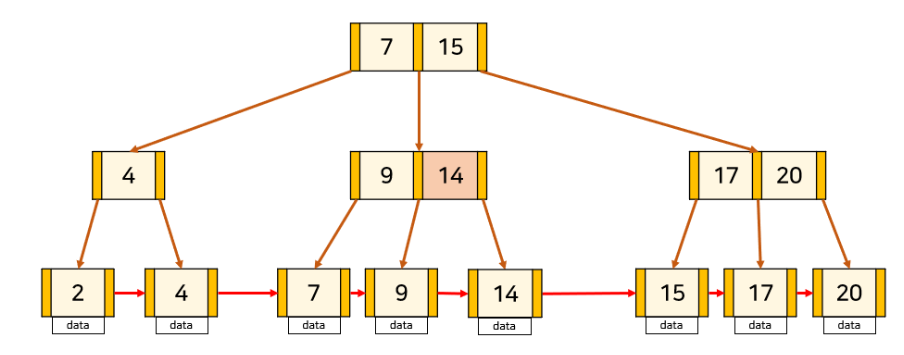
24 삭제

삭제의 경우 

1)key를 삭제한다

->삭제한 값이 최소값일 경우 부모 노드 값을 수정한다

2)key의 최소 개수보다 작으면 형제 노드에게서 하나 가져온다

-> 좌측 노드에게서 가져왔다면 부모 노드의 좌측 key를, 우측에서 가져왔다면 우측 key를 수정한다

3)형제 노드도 최소일 경우 두 노드를 병합한다

-> 두 노드의 공통 부모 key 값을 삭제한다

 

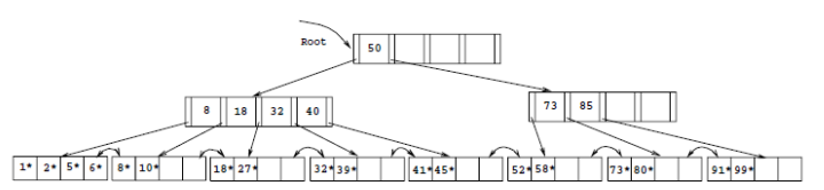
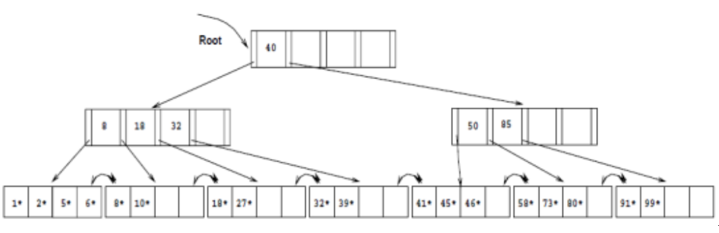
46추가, 52 삭제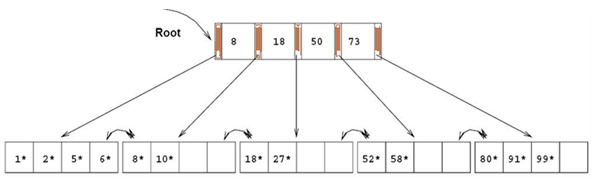

 

32, 39, 41, 45, 73 삭제

부모 key 값을 삭제했을 때 해당 노드의 key 값도 최소 이하가 된다면,

해당 노드와 형제 노드 하나, 그리고 두 노드의 공통 부모 key를 merge한다

이때 key 개수가 최대 개수보다 많으면 중앙 값을 올려 부모 노드로 올리고 (위 경우)

최대 개수 이하면 그대로 사용한다 (아래 경우)

 

 

 

 

+ISAM tree

동적인 B-tree와 달리 isam tree는 정적이다

트리의 구조는 변하지 않고 추가되는 데이터는 overflow page로 관리한다

트리를 변경하지 않으므로 데이터의 삽입과 삭제가 빠르지만

오버플로우 페이지는 물리적으로 정렬되지 않아 탐색 속도는 느리다

 

 

 

 

+Bulk Loading

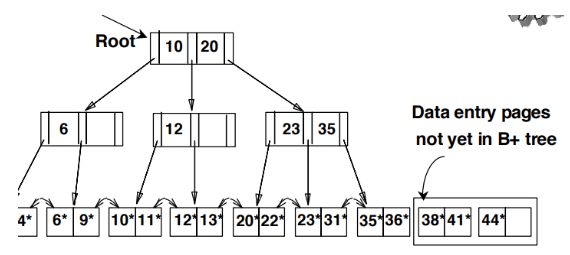
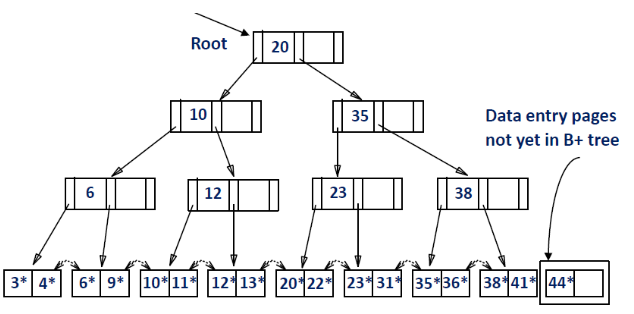
b+tree는 key를 삽입시 트리를 수정해야하므로 overhead가 크다

-> 삽입할 데이터를 모아서 정렬, 순서대로 삽입

= 데이터가 우측 하단에 순서대로 들어가므로 좌측 부분은 수정 x = overhead 감소

 

 

 

 

 

 

https://rebro.kr/169

[DB] 10. B-Tree (B-트리)

https://rebro.kr/167

[DB] 11. 인덱스(Index) - (1) 개념, 장단점, B+Tree 등

https://en.wikipedia.org/wiki/B%2B_tree#Insertion

B+ tree - Wikipedia

https://bb-library.tistory.com/162

[데이터베이스] ISAM과 B+ 트리

가장 깔끔하게 정리된 글

https://moondol-ai.tistory.com/204

DB 무결성제약조건(Integrity Constraints) & Normalization & B+-Tree

https://www.chegg.com/homework-help/database-management-systems-3rd-edition-chapter-10-solutions-9780072465631

예제 문제